Using models in junior secondary Science
Models are referenced throughout the Australian Curriculum in junior secondary Science – and have gained even more prominence in version 9 of the curriculum. They’re a great teaching tool. Whether you use them to demonstrate a concept to students, or get students to create and use their own, models can be a powerful way to support students to develop, apply, and consolidate their learning.
So what is a model?
‘Model’ is a vague term in Science; it can be any representation of a system of events, ideas, or processes. It can also be physical, conceptual (such as a diagram or flow chart), or mathematical (such as an equation). A good model is both accurate and simple, and can be used to show relationships and trends, or to make predictions.
Overall, models are just a representation, so they can’t be completely accurate.
Most models can’t include every complex interaction or every detail, which can limit their real-world application. But we can’t always bring the real-world into the classroom. Instead, we rely on models to help us focus on, and explain, key ideas – in particular with subjects like Science where the concepts are often complex or theoretical. So models will always be a large part of Science, which is why we ask students to use them. Here we explore 3 types of models - Physical, Conceptual and Mathematical.
Types of models in science
Physical models
These are a physical replica of something, and are sometimes (but not always) to scale. It might be a model of Earth’s layers, a model of an ecosystem, or using a molecular model kit to show compounds and molecules.
Limitations: Physical models usually can’t include every detail – if using a model of a cell to represent the surface area of a mitochondrion it won’t be accurate, as the model won’t include every fold of the membrane.
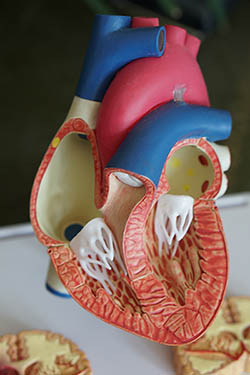
Conceptual models
These are a ‘model of a concept’ – like a flow chart representing a food chain or web, or a force diagram of a skydiver, or ‘a model that is conceptual’ – like representing atoms in a Bohr model.
Conceptual models can be very simple, like a chain of events, or display complex interactions within a system. Often we ask students to model relationships within a concept by making a mind map.
Limitations: Some concepts are too complex to represent as the model would get too large and confusing. This means you would need to sacrifice accuracy for simplicity and focus, which makes the model less detailed but can still be useful.

Mathematical models
This is when real life concepts are represented using mathematics. This could be as simple as an equation (such as molarity or chemical reaction equations), but can then be combined with graphs and diagrams (which are conceptual models). For example, you can use an equation to calculate the amount of force needed to push a truck up a hill and then represent the forces on a force diagram, or use equations to calculate reproductive strategies and then graph the different strategies against the carrying capacity of the ecosystem. Mathematical modelling is also used to predict the weather – over a hundred years of data is analysed to help you decide if you want to risk having a picnic on a day with a 60% chance of rain!
Limitations: Mathematical models only take into account the specific variables that are being modelled. In reality, there are many more potential variables that would affect the results. For example, you can use mathematical equations and diagrams to model forces, but in reality there may be other factors affecting the object that make your calculations inaccurate (such as the amount of drag changing as a skydiver changes arm and leg position).

Let’s not forget our favourite type of model – the meme. Essentially, memes are a conceptual model using metaphor or analogy to make a point (or sometimes not). We know there’s no shortage of these in teaching.


